Class 1 05/06/2019
Fibonacci numbers
Fibonacci numbers (Exponential Algorithm)
1 | 0, 1, 1, 2, 3, 5, 8, 13, 21 |
Code
1 | fib1(int n) { |
Time Complexity
Answer O(2^n)
Less intuitive, not like1
2for i in range(10):
a[i] = a[i-1] + 2
Recursion Tree
$ T(n) = \text {runtime of fib1(n)}$
1 | T(n) |
When hit 0 or 1, the recursion ends.
1 | /\ |
1 | in first half of this tree |
Thus we have
$ 2 ^ {n/2} <= T(n) <= 2 ^ n $
Therefore
$ 2 ^ {n/2} = (\sqrt {2}) ^ n ~= 1.4n $
Clearly, this is a bad time complexity algorithm.
1 | T(n) |
Linear algorithm
Code
1 | fib2(int n) { |
Time Complexity
Linear time: O(n)
Constant space algorithm
Code
1 | fib2(int n) { |
Analysis
1 | i varies between 0 and 1 |
Matrix solution
Idea
$$
A = \left[
\begin{matrix}
1 & 1 \
1 & 0
\end{matrix}
\right]
$$
$$
A^2 = \left[
\begin{matrix}
1 & 1 \
1 & 0
\end{matrix}
\right] *
\left[
\begin{matrix}
1 & 1 \
1 & 0
\end{matrix}
\right] =
\left[
\begin{matrix}
2 & 1 \
1 & 1
\end{matrix}
\right]
$$
1 | A = | 1 1 | = | a2 a1 | |
Time Complexity
Basic: O(n)
Optimized: O(logn)
Strategy
Since we are dealing with A^n, the optimized time complexity of pow(x, n) is O(logn)1
2
3
4A^n = |A(n/2)^2 | n is even
|A((n-1)/2)^2 * A | n is odd
A^64 = (A^32)^2 = ((A^16))^2^2 = A^(2^6)
Asymptotic Notation
Comparison of each notation
| Compare Function Growth | Compare Numbers | f(n) = 5n | g(n) = n^2 |
|---|---|---|---|
| O | <= | f(n) = O(g(n)) | |
| o | < | f(n) = o(g(n) | |
| Θ | = | for f(n) = 100n | and g(n) = n + 100 |
| Ω | >= | f(n) = Ω(g(n)) | |
| ω | > | f(n) = ω(g(n)) |
Mathematical Derivation
f(n) = O(g(n))1
2iff exists constants C and n0
s.t. when n > n0, f(n) <= C * g(n)
1 | lim(n->inf) f(n)/g(n) = 0 | fn = O/o(g(n)) |
Practice:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20lim(n->inf) (100n)/(n+100) = 100
fn = O/Θ/Ω(g(n))
f(n) = nlgn g(n) = n^2
f(n) = O/o(g(n))
f(n) = 2^n g(n) = 3^n
f(n) = O/o(g(n))
lim(n->inf) f(n)/g(n) = lim(n->inf) (2/3)^n = 0
f(n) = n+3 g(n) = 2 * sqrt(n)
f(n) = Ω/ω(g(n))
f(n) = log2(n) g(n) = log3(n)
f(n) = Ω/O/Θ(g(n))
lim(n->inf) f(n)/g(n) = lim(n->inf) log2n/log3n = log3/log2
f(n) = (logn)^2 g(n) = log(n^2) = 2logn
f(n) = Ω/ω(g(n))
Master’s Theorem
Idea of merge sort
T(n) = 2T(n/2) + n
1 | T(n) n | n |
Time Complexity of merge sort
T(n) = height T(level) = logn n = nlogn
Master’s Theorem
1 | T(n) = a * T(n/b) + n^c, where a, b, c are constants |
Now we have to compare logb(a) and c
- logb(a) > c, T(n) = Θ(n^(logb(a)))
- logb(a) = c, T(n) = Θ((n^c) * logn)
- logb(a) < c, T(n) = Θ(n^c)
Practice1
2
3
4
5
6T(n) = T(n/2) + 1 T(n) = Θ(lgn)
T(n) = 8T(n/2) + n^2 T(n) = Θ(n^3)
T(n) = 7T(n/2) + n^2 T(n) = Θ(n^(log2(7)))
T(n) = 4T(n/2) + n^2 T(n) = Θ(n^2 * (logn))
T(n) = T(n/2) + n T(n) = Θ(n)
T(n) = T(n-1) + n (Not master's theorem)
Draw the Recursion Tree of the last one1
2
3
4
5
6
7
8
9
10
11
12
13Recursion Tree of T(n) = T(n-1) + n
T(n) n
T(n-1) n-1
T(n-2) n-2
...
T(1) 1
T(n) = 1 + 2 + 3 + ... + n = n(n+1)/2
Θ(n) = n^2
Other useful Summation Formula
1 | 1 + 2 + 3 + .. + n = n(n+1)/2 |
Normal case
T(n) = T(n/3) + T(2n/3) + n
1 | T(n) n | n |
1 | /\ |
Time Complexity of Normal recursion tree
T(n) = Θ(nlgn)
Some examples
1 | T(n) = T(n/4) + T(3n/4) + n T(n) = Θ(nlgn) |
Quick Sort
Partition
1 | Given array like |
Code
1 | QuickSort(int[] A, int i, int j) { |
Time Complexity
1 | T(n) = 2T(n/2) + n = Θ(nlogn) |
Average T(n) = Θ(nlogn)
Worst T(n) = Θ(n^2)
Code of Partition
1 | pivot = A[j] |
A[cur] > pivot
1
cur += 1
A[cur] <= pivot
1
2
3swap(A[cur], A[p+1]);
p += 1;
cur += 1
1 | Partition(int[] A, int i, int j) { |
Class 2 05/13/2019
Review
Review of quicksort
Stable Sort
1 | | ... | 5(1) | ... | ... | 5(2) | ... | |
Runtime of Quick Sort
Runtime:
Average: $O(nlogn)$
Worst: $O(n^2)$
The worst case is $T(n) = T(n-1) + n$
Pivot Selection
- Median of Three
1 | | i | ... | (i+j)/2 | ... | j | |
Heap Sort
Types of Heap
- Max Heap
- Min Heap
Operations (of Heap)
- Insert(E) $O(logn)$
- getMax() $O(1)$
- deleteMax() $O(logn)$
Operations (of Sorted Array)
- Insert(E) $O(n)$
- getMax() $O(1)$
- deleteMax() $O(1)$
Comparison of array and heap
The worst time of heap operation is logn.
However, A sorted array takes On time to insert, which is the bottleneck of the overall time complexity.
Logical View and Physical View
Logical View1
2
3
4
5
6
7
8
9
7(1)
/ \
3(2) 6(3)
/ \ /
1(4) 2(5) 5(6)
Almost-Full Binary Tree
Parent must be >= both children
Physical View
1 |
|
helper functions of heap
i is the index
parent(i) = i / 2leftChild(i) = i 2rightChild = i 2+1
getMax() O(1)
getMax() - return A[1]
insert() O(logn)
Case 1
1 | 7(1) |
Case 2
1 | 7(1) |
Code of insert()
1 | void insert(int e) { |
deleteMax()
1 | 8(1) |
heapify()
1 | 6(1) |
Code of heapify()
1 | void heapify(int[] A, i) { |
Code of deleteMax()
1 | void deleteMax() { |
Heap Sort
Max Heap1
2
3
4
5
6
7
8
9 1 2 3 4 5 6
Array | 7 | 3 | 6 | 1 | 2 | 5 |
Pretend we are deleting the max val.(deleteMax())
1 2 3 4 5 || 6
Array(after deleted) | 5 | 3 | 6 | 1 | 2 || 7(max) |
Now we get the biggest node in the tail of the array.
continue sort the rest.
Code of Heap Sort
1 | void heapSort(int[] A) { |
makeHeap()
Solution 1 insert n times O(nlogn)
Solution 2
1 | 6(1) |
Code of makeHeap()
1 | // On time |
Example of heap sort
1 | First, make this into a heap. |
Sorting Algorithms
Types of sorting algorithms
| Algorithm | Time Complexity | Notes |
|---|---|---|
| Quick Sort | $O(nlogn)$ | |
| Merge Sort | $O(nlogn)$ | |
| Heap Sort | $O(nlogn)$ | |
| Bubble Sort | $O(n^2)$ | |
| Insertion SOrt | $O(n^2)$ | |
| Selection SOrt | $O(n^2)$ | |
| Counting SOrt | $O(n)$ | Non-comparison based |
| Radix SOrt | $O(n)$ | Non-comparison based |
Theorem of comparison based sorting algorithm
Comparison based sorting algorithm always run in $Ω(nlogn)$.
Counting Sort
1 | Assume we have array A |
Code of Counting Sort
1 | //Step of counting sort |
problems of Counting Sort
Q: Why 0-based?
A: To represent the case where the input has 0.
Q: what happened if we have negative input?
A: Map the input to the form we want. e.g. [-10, 10] -> [0, 20]
Q: Is this algorithm stable?
A: In this case, yes.
Analysis of Counting Sort
Run time: $O(n+k)$
Space: $O(k)$
Radix Sort
Introduction
Also known as digit sort.
Only for positive base 10 integers.
Example
1 | Use the counting sort to sort the colomn |
Analysis
d is the number of digits, k is the range of the inputs(e.g. 32 bit integer)
Run time: $O((n+k)d)$
Space:
e.g.1
2
3
432-bit int
| 8-bit | 8-bit | 8-bit | 8-bit |
d = 4 times of counting sort
k = 2^8 = 256
Class 3 05/20/2019
Questions about Order Statistics
Given a collection of integers, get the min/max value, median, 25% element, rth smallest element, etc.
Question: How do we find the rth smallest element?
Solution1 Sort the array
- sort array
- return A[k]
The run time should be O(nlgn)
Solution2 Based Partition
Idea
1 | Definition 2 |
Code
1 | // definition 1 |
Analysis
$ T(n) = T(n/2) + n = O(n)$
1 | Example |
Find Top K
Solution 1 Sort the array
- Sort the array
- return A[1:k]
Time: $ O(nlogn) $
Solution 2 findKth algorithm
- partition
- return A[1:k]
Time: $ O(n) $
Solution 3 Min Heap
- make a min heap
- delete k times
Time: $O(n + klogn)$ (depends on which one’s bigger)
Solution 4 Max Heap
- m make a max heap A[1:k]
1 | for (i = k+1, ... , n) |
Time: $ O(k + (n-k)*logk)$
When n is large, $ O(nlogk) $
When k is large, $ O(k) $
Big Integer Multiplication
for integers of 32-bit(unsigned), we have a range of $ (0, 2^{32}-1) $, which are 10 digits
for integers of 64-bit(unsigned), we have a range of $ (0, 2^{64}-1) $, which are 10 digits
RSA
An encryption algorithm using large integer multiplication.
Idea
Input: 2 integers of n-bits
Example:
1 | 1110 = 14 |
Time : $ O(n^2) $
Divide and Conquer
a can be split to a1 | a2
for example,
a = 1110 = $ 11 * 2^2 + 10 $ (Shift left by 2 bit)
Therefore,
$ a = a_12^{n/2} + a_2 $
$ b = b_12^{n/2} + b_2 $
$ a b = a_1b_12^{n} + (a_1b_2+a_2b_1)2^{n/2} + a_2b_2 $
We divide the 1 problem to 4 child problem.
T(n) = 4T(n/2) + n(sum 2 n-bit integers) = O(n^2)
Improve the running time
$ p_1 = a_1b_1$
$ p_2 = a_2b_2$
$ p_3 = (a_1+a_2)(b_1+b_2)$
$ a b = p_12^{n} + (p_3-p_1-p_2)2^{n/2} + p_2 $
We can save the Time to
T(n) = 3T(n/2) + n
$ T(n) = O(n^{log_2{3}}) $
Extra cases
What if 2 integers are not with the same digits?
Pad the 0’s to the nearest exponential of 2.
1 | For example |
Square Matrix Multiplication
Idea
input: 2 n*n matrices
$
X = \left[
\begin{matrix}
A & B \
C & D
\end{matrix}
\right]_{n*n}
$
$Y = \left[
\begin{matrix}
E & F \
G & H
\end{matrix}
\right]_{n*n}
$
$ X*Y = O(n^3) $
Here we use the block of matrix to Divide & Conquer
$
X = \left[
\begin{matrix}
1 & 1 \
1 & 0
\end{matrix}
\right]_{n*n} = \left[
\begin{matrix}
A & B \
C & D
\end{matrix}
\right]
$
$Y = \left[
\begin{matrix}
1 & 1 \
1 & 0
\end{matrix}
\right]_{n*n} = \left[
\begin{matrix}
E & F \
G & H
\end{matrix}
\right]
$
$ XY = \left[
\begin{matrix}
{AE+BG} & {AF+BH} \
{CE+DG} & {CF+DH}
\end{matrix}
\right]_{nn}
$
Therefore, $ T(n) = 8T(\frac{n}{2}) + n^2 = O(n^3)$
Optimization
$ XY = \left[
\begin{matrix}
{AE+BG} & {AF+BH} \
{CE+DG} & {CF+DH}
\end{matrix}
\right]_{nn} = \left[
\begin{matrix}
{Q} & {R} \
{S} & {T}
\end{matrix}
\right]
$
$Assume:$
$P_1 = A(F-H)$
$P_2 = H(A+B)$
$P_3 = E(C+D)$
$P_4 = D(G-E)$
$P_5 = (A+D)(E+H)$
$P_6 = (B-D)(G+H)$
$P_7 = (A-C)(E+F)$
$Q = P_4 + P_5 - P_2 + P_6$
$R = P_1 + P_2$
$S = P_3 + P_4$
$T = P_1 + P_5 - P_3 - P_7$
$ X*Y = \left[
\begin{matrix}
{AE+BG} & {AF+BH} \
{CE+DG} & {CF+DH}
\end{matrix}
\right] = \left[
\begin{matrix}
{P_4 + P_5 - P_2 + P_6} & {P_1 + P_2} \
{P_3 + P_4} & {P_1 + P_5 - P_3 - P_7}
\end{matrix}
\right]
$
Therefore, $ T(n) = 7T(\frac{n}{2}) + n^2 = O(n^3)$, Successfully optimized.
Counting Inversions
Idea
1 | Inversion: if i < j && A[i] > A[j], then (i, j) is an inversion. |
Max num of inversions of a n list is $ C^{2}_{n} = O(n^2) $
Code
1 | // Brute force |
Better Implementation
1 |
|
Code
1 | int CountInv(int[] A, int begin, int end) { |
Analysis
$ T(n) = 2T(\frac{n}{2}) + nlogn = O(nlognlogn)$
Optimization
1 | int CountInv(int[] A, int begin, int end) { |
$ T(n) = 2T(\frac{n}{2}) + n = O(nlogn)$
Example
1 | | 7 | 2 | 3 | 4 | 1 | 6 | 5 | 8 | |
Class 4 06/03/2019
Binary Search Tree and Hashtable
Difference between two data structures
| Hashing | BST | |
|---|---|---|
| O(1) | h | insert(key,value) |
| O(1) | h | lookup(key) |
| O(1) | h | delete(key) |
| amartized running time | O(logn) basically | |
| support traversing by ordered keys |
Binary Search Tree
Definition
1 | class Node { |
1 | 5 |
- Left subtree is BST
- Right subtree is BST
- root.key > all keys in left subtree
and root.key < all keys in right subtree
Tree Traversals
- Level-order
- Pre-order
- Post-order
- In-order
Level-order Traversal
1 | void LevelOrder(Node root) { |
Right Side View Question
1 | 5 |
1 | // we can just modify the original code by |
Pre-order Traversal
1 | void PreOrder(Node cur) { |
In-order Traversal
1 | 5 |
Represent duplicate keys in BST
Requirement
Has to support root >= all left and root < all right.
- MultiSet
- MultiMap
1 | 5 |
Implementation
Lookup
1 | boolean Lookup(Node cur, int key) { |
Insert
1 | Node insert(Node cur, int key, String val) { |
Delete
1 | 5 |
Case 1: No children
update parent’s reference
Case 2: Single child
Parent pointing to child
Case 2: two children
- find predecessor p
- swap
- delete recursively
1 | # Definition for a binary tree node. |
Class 5 06/10/2019
Recap of BST
Predecessor and Successor
Logical view
1 | 5 |
Predecessor
- case1: rightmost node of the left subtree
- case2: find smaller node on the ancestor path
Re-Definition of node
1 | class Node { |
Find Kth key in BST
Idea of In-order traversal
We can find the kth key by stopping at kth step during in-order traversal.
Our goal is to control the time in O(h).
Re-definition of Node
1 | class Node { |
Logical View
1 | 5(5) |
Code
1 | int kth(Node root, int k) { |
Example
1 | 5(5) |
Hashing/ HashTable
Pre-hash and Hash
Difference
| Pre-Hash | Hash |
|---|---|
| int/float/string/user-define -> int | arbitrary large int -> reasonable int |
| Can only return small integers |
Example
HashTable<String , T> means we have String as key, T as value.
1 | class Pair { |
HashTable<Pair, T> means we represent a coordinate as key.
In java, we overwrite the HashCode() as the pre-hash function.
For a String , a practical pre-hash function would be calculating the ascii code.
ASCII is a 8 bit representation of a char data type.
e.g.
For “hello” and “hell”, we have1
2Hashcode("hello") = 'h' * 41^3 + 'e' * 41^2
+ 'l' * 41^1 + 'l'
p.s. the hashcode of single letter depends on the encoding way. If simple english, we just use its ascii. If unicode, we use another way.
e.g. To represent Pair, we can use x^y as its hash function.
SubSet : We can split the string and calculate each part of it, while we have a bigger chance to collision and worse time consumption.
Caching : For extra long String, we can only call the hash function once, and store the pre-hash value in the memory.
HashTable
Idea
key = Integer[in large space]
Suppose key ranges from (0, m-1), then we have to map the integer from 0 to m-1
insert(key)
hash: int -> int [0, m)
How do we choose m?
m changes dynamically
Load Factor $ \alpha = n/m $
n = number of k-v pairs
m = size of current hashtable
Here, we increase m exponentially.
e.g. m = 1024, next m would be 2048
Question: Why don’t we increase m by 100 each time?
Answer: Suppose we have $ \alpha = 1$, then every time we hit the bottle neck, we have to find a continuous memory to store all the stuff, which is a expensive On operation.
Question: what happens if we do insert n times with m increasing by 100?
Answer:1
2
3
4
5
6
7
8
9
10
11
12
13C, C, C, ..., C, 100C
C, C, ..., 200C
C, C, ..., 300C
C, C, ..., n/100C
Overall: 100 + 200 + 300 + .. n/100 ~= O(n^2) time, which is super expensive.
C, C, C, ..., C, n/lognC
C, C, ..., n/8C
C, C, ..., n/4C
C, C, ..., n/2C
Overall: n/logn + n/8 + n/4 + .. n/2 ~= O(n) time, which is much better.
Question: what happens if we have to adjust the size?
Answer: Suppose $ \alpha < 0.2$, we would like to shrink the size by half. If $ \alpha > 0.8$, we would like to double the size. The threshold shold be decided wisely.
what should be the hash function?
hash function: (large space)int -> int [0, m)
Division Method
$ H(x) = x \% m $
If m is a power of 2, then this function is bad. e.g. If m = 1024, if pre-hash only consists of even numbers, then half of the space is wasted. We should pick prime number as m. (disadvantage)
Multiplication Method
$ H(x) = a * x \% 2^{32} >> (32 - r) $
$ m = 2^r $
a is constant chosen randomly.
Explanation: Since m = 2^r, we only need r bit to represent the hashcode. Suppose x is 32 bit, and a is 32 bit, then a*x is 64 bit. Then we mod it by 2^32, where we throw away half of the number. Next we right shift till we get only r digits, so that the hashtable con contain the num.
1 | x = | 1 | 1 | 0 | ... | 1 | 0 | 1| (32) |
Collision
Birthday Paradox
Suppose we randomly select x people, what’s the probability that two people have same birthday?
To get a 50% of prob, we should select 23 people.
This example showws the impact of collision.
There are 2 ways to deal with collision, Chaining, Probing.
Chaining
$ h(x_{1}) = k $
$ h(x_{2}) = k $
Then we have key k -> $x_1$ => $x_2$
run time O(1 + $ \alpha $)
$ \alpha $ is load factor n/m
worst case insert: len n/m logn
Probing
Here we are talking about Linear Probing.
$ h(x_{1}) = k $
$ h(x_{2}) = k $
Then we have key k ($x_1$) -> n slots taken -> (k+n) $x_2$
Delete: When wew delete an element, all the following elements have to be re-hashed.
Suppose $ \alpha = n/m = 0.1$
90 % of time is empty
Therefore we need $1 / (1-\alpha)$ space to get a slot.
time complexity: O n
Class 6 06/17/2019
Dynamic Programming
Steps of DP problem
Situations of DP
- Optimization : max/min problem
- Counting: binomial
- Feasibility: if the target is possible to get
Design recursion
Naive recursive implementation yields bad running time(Usually exponential)
- e.g. Recompute the same thing. Fibonacci.
Caching
- bottom -> up( small -> large)
- top -> down with memoization
Longest Common Subsequences
Description
1 | input: A[1 ... n] |
Solution
1 | define f(i, j) = length of the LCS given A[1 ... i] & B[1 ... j] |
Pseudocode
1 | // O 2^n time O m+n space |
Code(Bottom Up)
1 | def func(A, B): |
1 | int lcs(int[] A, int[] B) { |
1 | List<Integer> constructSolution(int[] A, int[] B, int[][] dp) { |
0-1 Knapsack Problem
Description
1 | Assume we have n items |
Pseudocode
1 | // O N*C time O n*c space -> O C space(optimized) |
Class 7 06/24/2019
Unbounded Knapsack
Description
Input: n types of items, for each type there are inf copies. For each item of type i, we have values[i] and weights[i]. We also have capacity of knapsack.
Naive approach
f(i) maximum value we can get
f(i) = max value given capacity i
1 | a1 = V[1] + f(i-w[1]) |
Pseudocode
1 | // O Cn time O C space |
Coin Change
Description
1 | Assume we have coins like |
Naive approach
1 | f(i) = min( |
PseudoCode
1 | int coinChange(int[] d, int n) { |
Knapsack with multiple constraints
Description
1 | Now the items have a volume constraint |
Recursion
1 | i = # of items of first i items |
Pseudocode
1 | // O(nWU) time O(nWU) space -> O(WU) space |
Palindrome
Description
1 | ana |
Recursion
1 | f(i) := min # of palindromes given A[1....i] |
Pseudocode
1 | // O n^3 time O n space -> O n^3 time to O n^2 time optimizing isPalindrome, O n space to O n^2 |
Class 8 07/08/2019
Matrix Multiplication
Description
1 | A1 * A2 * ... * An |
Solution
Explanation
1 | f(i, j) = min cost to multiply Ai * .. * Aj |
Pseudocode
1 | // O n^3 time O n^2 space |
Sell products problem
Description
Assume we have a street of n houses, we have 3 colors of them, red, green and yellow. The profit of coloring them should be R[], G[], Y[]. We want to have maximum profit while coloring all n houses. No adjacent houses can be painted the same color.
Solution
Explanation
We assume g(i) = best way to color 1 … i, with ith house colored as green
r(i) = paint first ith house and last house is red
y(i) = same as above
g(i) = G[i] + max(r(i-1), y(i-1))
r(i) = R[i] + max(g(i-1), y(i-1))
y(i) = Y[i] + max(r(i-1), g(i-1))
r[1] = R[1]
g[1] = G[1]
y[1] = Y[1]
Pseudocode
1 | int maxProfit(int[] G, int[] R, int[] Y) { |
Class 9 07/10/2019
Matrix problem
Description
Given n * n grid filled with positive integers, we want to find longest increasing path.
1 | 3 2 1 |
Solution 1((Bottom up))
1 | 3 5 1 |
Solution 2(Top down)
1 | // Top down approach, O(mn) time |
Solution 3 (Graph & Toposort)
We can do a topological sort on this graph, in which small vertices point to bigger vertices. Then we start doing topo sort with indegree[0] nodes and search longest path. The maximum level of searching is the longest length of this increasing path.1
2
3
4
5
61 -> 3 -> 2
| | |
7 <- 5 -> 8
| | |
2 <- 1 -> 4
Directed Graph
Longest Increasing Subsequence
Description
Given an array 1, 2, 4, 3, find the longest increasing subsequence, 1, 2, 3
Solution
Explanation
1 | f(i) = length of LIS given A[1:i] |
Pseudocode
1 | def func(A): |
Edit Distance
Description
Given str1 and str2, we can do insert, delete and replace, find the shortest operations we need to turn str1 to str21
2
3"abc" -> "abch"
"abc" -> "ab"
"abc" -> "abh"
Solution
Explanation
1 | f(i, j) = edit distance if given A[1:i] and B[1:j] |
Pseudocode
1 | int editDistance(String A, String B) { |
Class 10 07/15/2019
Graph Introduction
Definition: G = (V, E)
Type: {directed graph, undirected graph}
Notation: |V| = n, |E| = m
DataStructure: {Adjacent List, Adjacent Matrix}
Storage: O(m+n) for Adj List, O(n^2) for Adj Matrix.
Time complexity
| Operation | Adjacency List | Adjacency Matrix |
|---|---|---|
| Existence of Edge | O(d) | O(1) |
| Traverse the node | O(d) | O(n) |
BFS
1 | BFS(G, S) { |
Analysis
Time: O(m+n) if we take initialization into account.
We would like to use Adjacency List here.
Word Ladder
Pseudocode
1 | BFS(graph[], start, end, dic) { |
puzzle - 8
Description
1 | 3 _ 5 |
Explanation
1 | As you can see, each state is a node.\ |
Pseudocode
1 | // helper function |
Connected Components(Undirected Graph)
Description
1 | 1 - 3 |
Pseudocode
1 | /** |
Counting islands
Description
1 | 1 1 0 0 |
DFS
1 | DFS(G, u, visited[]) { |
Connected Components
1 | DFS_ALL(G) { |
Cycle Detection
1 | // O 2^m time |
Class 11 07/22/2019
Review
Time Complexity of some algorithms
| Algorithm | Time Complexity |
|---|---|
| BFS | O(m+n) |
| Connected Components | O(m+n) |
| DFS | O(m+n) |
| Cycle Detection | O(m+n) |
DAG
- DAG = Directed Acyclic Graph
- Topological Sort
Topological Sort
DFS Solution
Idea
1 | G = [[1, 3], [2, 5], [2, 6], [4, 2], [4, 3], [3, 6]] |
Step
Use DFS_ALL() find finish time.
Sort vertices by finish time in decreasing order.
Doesn’t work for cyclic graph. Will stuck in the recursion forever.
Pseudocode
1 | // We mark each node in the order we visit them |
Non DFS Solution
Idea
Record the indegree of the vertices and keep searching and updating the indegree map.
The running time is O(m+n)
Pseudocode
1 | TopoSort(G) { |
Boggle
Description
1 | Given a 4X4 board |
PseudoCode
1 | // 4^16 Time Complexity. Terrible. |
1 | def getWords(root): |
SCC
Description
Every node in this group have access to any other nodes.
| d | c |
|---|---|
| Strongly connected components | u->v and v->u |
| Weakly connected components | u->v or v->u |
Example
1 | G = [[1, 3], [3, 2], [2, 1], [2, 4], [4, 5], [5, 4], [4, 6], [6, 7], [7, 8], [6, 8], [7, 9], [8, 9], [9, 6]] |
Steps
- Do topological sort on G(DFS)
- BFS in GT using sequence produced by step 1
SSSP
Description
SSSP = single source shortest path
given Graph, we need to find every shortest path from the source S to other nodes.
Pseudocode
| negative weighted edges | DAG | not DAG | Time |
|---|---|---|---|
| N | SP on DAG, O(m+n) | Dijkstra’s algo | Omlogn(sparse) or O n^2(dense) |
| Y | Same as above | Bellmen Ford | O(mn) |
Class 12 07/29/2019
Single Source Shortest Path
Description
Given G and s, return a dist[u] which stores the shortest disatnce from s to u.
Shortest Path on DAG
Description
1 | input: G(V, E), S |
PseudoCode
1 | // helper function, check if v is the shortest path given u. |
Example
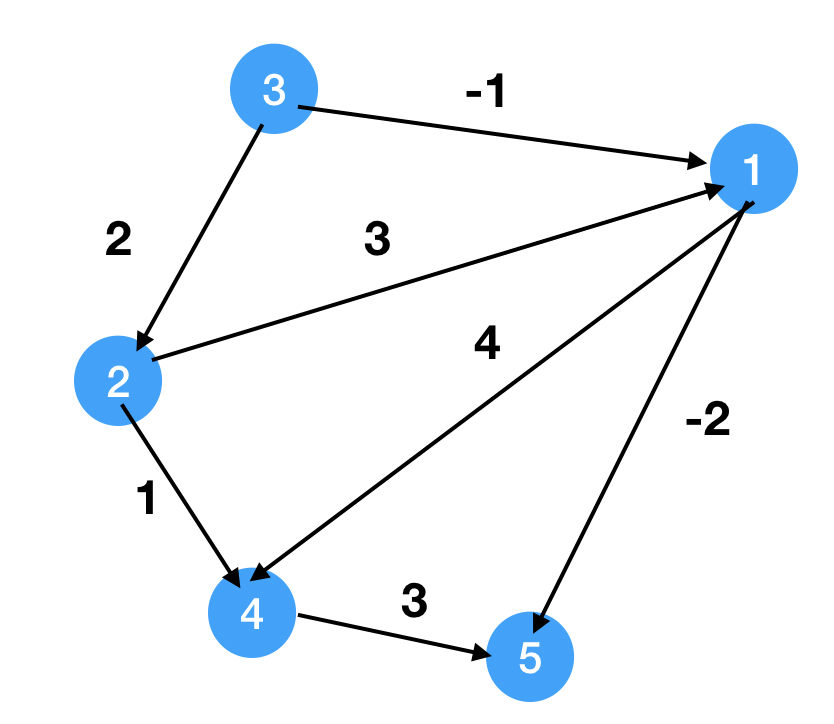
1
2
3
4
5
6
7
8
9topo = [3, 2, 1, 4, 5]
dist = [inf, inf, 0, inf, inf]
-1, 2 , 0, inf, inf 3
-1, 2, 0, 3 , inf 2
-1, 2, 0, 3 , -3 1
-1, 2, 0, 3 , -3 4
-1, 2, 0, 3 , -3 5
Q: Why is Topological sort working?
dist[u] = min(dist[x] + Cxu, dist[y] + Cyu), Assume x and y is before u. We need to finish all prerequisites before we try to update u, which is sorted by topological sort.
Dijkstra’s algorithm
Description
1 | Get the dist[], N is set of the vertices we vistited. |
Example
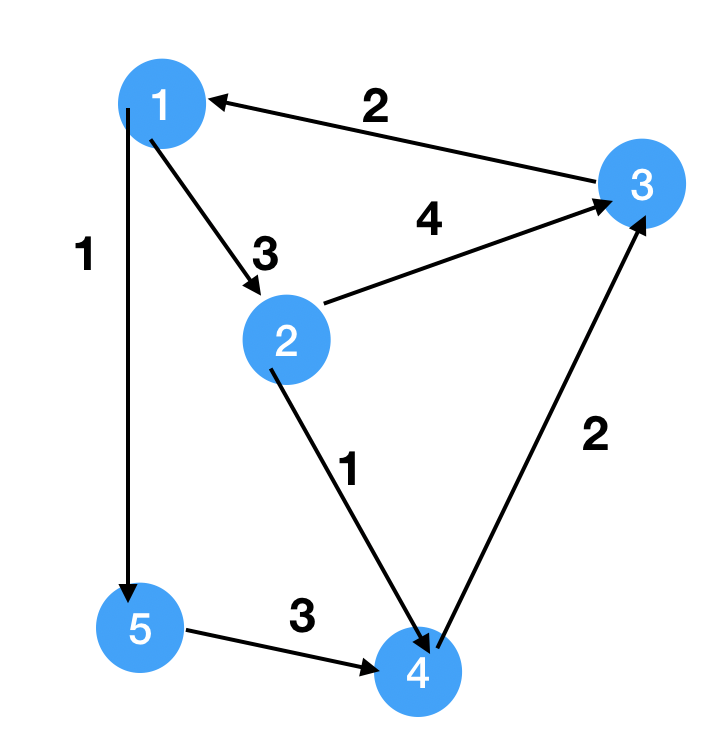
1
2
3
4
5
6
7
8
9S = 2
N = {}
dist = [inf, 0, inf, inf, inf]
1. u = 2, N = {2}, relax(2, 1), relax(2, 3), dist = [inf, 0, 4, 1, inf]
2. u = 4, N = {2, 4}, relax(4, 3), dist = [inf, 0, 3, 1, inf]
3. u = 3, N = {2, 4, 3}, relax(3, 1), dist = [5, 0, 3, 1, inf]
4. u = 1, N = {2, 4, 3, 1}, relax(1, 2), relax(1, 5), dist = [5, 0, 3, 1, 6]
4. u = 5, N = {2, 4, 3, 1, 5}, relax(5, 4), dist = [5, 0, 3, 1, 6]
Analysis
1 | 1. pick a smallest distance node, O(n) |
Bellman Ford
Description
Relax all edges n-1 times.
Example
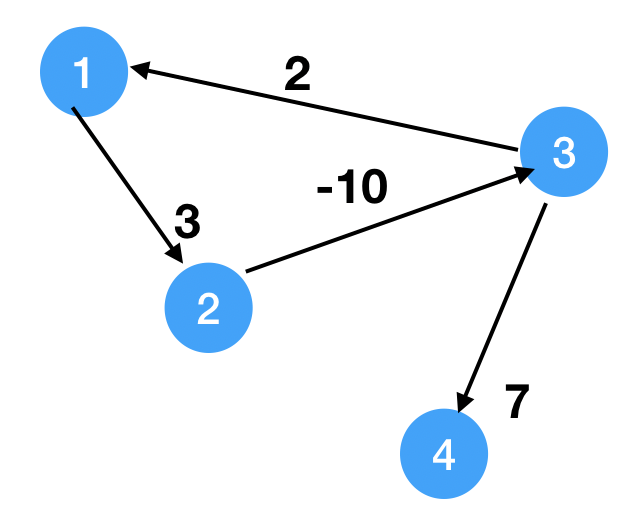
1
2
3
4
5
6
7S = 1
dist = [0, inf, inf, inf]
i = 1, we get 2, 3, 4, 1, dist = [0, 3, inf, inf]
i = 2, we get 2, 3, 4, 1, dist = [0, 3, -7, 0]
i = 3, dist = [0, 3, -7, 0]
Since we can at least update one true shortest distance at each loop, then we need at most n-1 times to update all true shorteset distances. After that, the dist array shouldn't change. If it changes, it means there's a cycle with negative weights.
PseudoCOde
1 | for (i = 1... n-1) {// we do the algo n-1 times |
Class 13 08/05/2019
Review
- Shortest path on DAG, O(m+n)
- Dijkstra’s Algorithm, O(mlogn) for pq, O(n^2) for matrix
Bellman Ford Algorithm, O(mn)
How do we track the actual paths? we need to modify the
relaxfunction.
1 | relax(u, v) { |
All Pair Shortest Path
Description
Goal: Build dist[u, v] = shortest distance from u to v
| negative weighted edges | DAG | not DAG | Time |
|---|---|---|---|
| N | O(mn) = On^2 ~ On^3 | Dijkstra’s algo | Onmlogn = O n2logn ~ n3logn or O n^3 |
| Y | m = n(n-1) at most | Bellman Ford | O(mn^2) = On3 ~On4 |
To improve the time complexity of Bellman Ford Algorithm interms of number of vertices, we can use Floyd-Warshall Algorithm.
Floyd - rWarshall Algorithm
Description
We define f_k(u, v) = shortest distance from u to v with only vertices{1, 2, … k} on shortest path
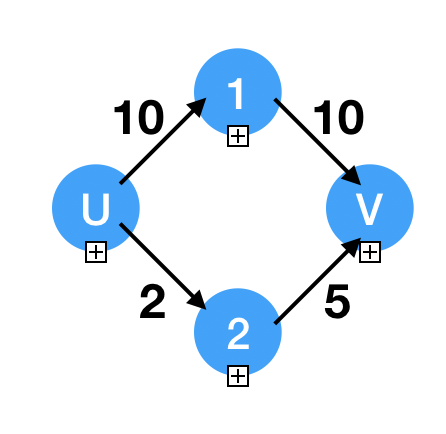
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17Example:
f_1(u, v) = 20
f_2(u, v) = 7
f_k(u, v) = cur, if (u, v) in E
inf, otherwise
base case:
f_0(u, v) = inf, if such edge doesn't exist
weight(u, v), otherwise
f(u, u) = 0
Recurrence:
f_1(u, v) = min(f_0(u, v), f_0(u, 1) + f_0(1, v))
f_k+1(u, v) = min(f_k(u, v), f_k(u, k+1) + f_k(k+1, v))
f_n(u, v) = true shortest distance {1, 2, 3, ..., n}
PseudoCode
1 | FW(G) { |
Example
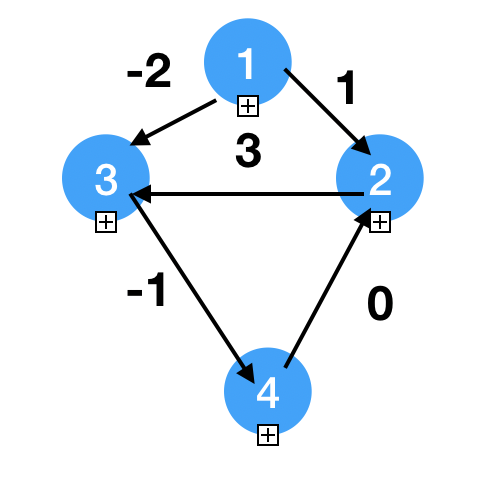
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35Adj matrix
0, 1, -2, inf
inf, 0, 3, inf
inf, inf, 0, -1
inf, 0, inf, 0
k = 1
dist[1, 1] = inf
dist[1, 2] = min(1, dist[1, 1] + dist[1, 2]) = 1
dist[1, 3] = min(-2, dist[1, 1] + dist[1, 3]) = -2
dist[1, 4] = min(inf, dist[1, 1] + dist[1, 4]) = inf
dist[2, 3] = min(dist[2, 3], dist[2, 1] + dist[1, 3]) = min(3, inf + (-2)) = 3
The first iteration basically doesn't change
k = 2
dist[1, 1] = min(inf, dist[1, 2] + dist[2, 1]) = inf
dist[1, 3] = min(-2, dist[1, 2] + dist[2, 3]) = min(1, 4) = 1
dist[4, 3] = min(inf, dist[4, 2] + dist[2, 3]) = 3
0, 1, -2, inf
inf, 0, 3, inf
inf, inf, 0, -1
inf, 0, 3, 0
k = 3
dist[1, 4] = min(inf, -2 + -1) = -3
dist[2, 1] = min(inf, 0 + inf) = inf
dist[2, 3] = min(3, 3 + 0) = 3
dist[2, 4] = min(inf, 3 + -1) = 2
...
Negative weighted cycle is not applicable!
Minimum Spanning Tree
Description
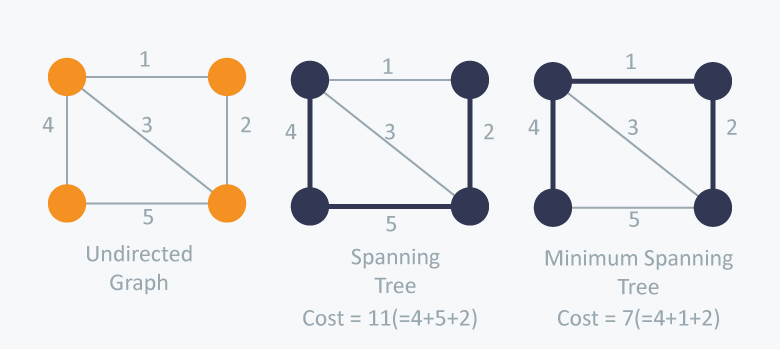
1
2
3Input: Connected undirected graph
we want to find a weighted undicted graph that has the smallest cost.
We have Prim's Algorithm and Kruskal's Algorithm to solve this.
Prim’s Algorithm
Description
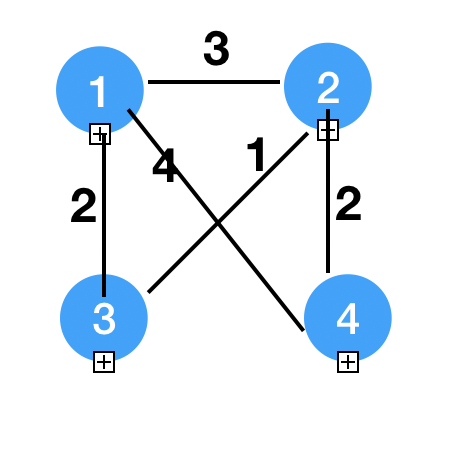
1 | N = {} |
Final Spanning Tree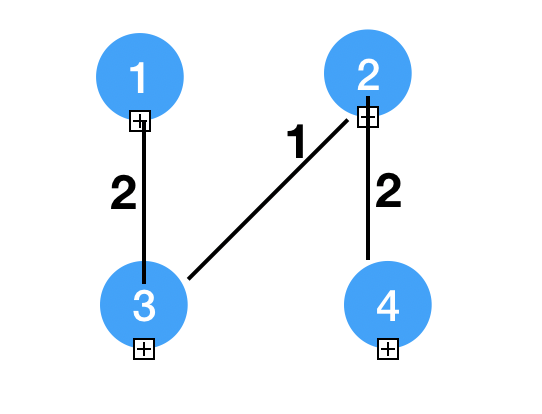
PseudoCode
1 | Prims(G) { |
Example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19N = {3}
dist = [2, 1, inf, inf]
parent = [3, 3, -1, -1]
N = {3, 2}
dist = [2, 1, inf, 2]
parent = [3, 3, -1, 2]
N = {3, 2, 4}
dist = [2, 1, inf, 2]
parent = [3, 3, -1, 2]
N = {3, 2, 4, 1}
dist = [2, 1, inf, 2]
parent = [3, 3, -1, 2]
Our Tree is (1, 3), (2, 3), (4, 2)
Actually here we don't need T here, and we can use a priority Queue to pick the smallest distance not in N.
Kruskal’s Algorithm
Description
1 | - Sort edges by their weights |
Disjoint Sets
1 | - We have n items {1, 2, ..., n} |
1 | // mlogn time |
Union Find
Logical View
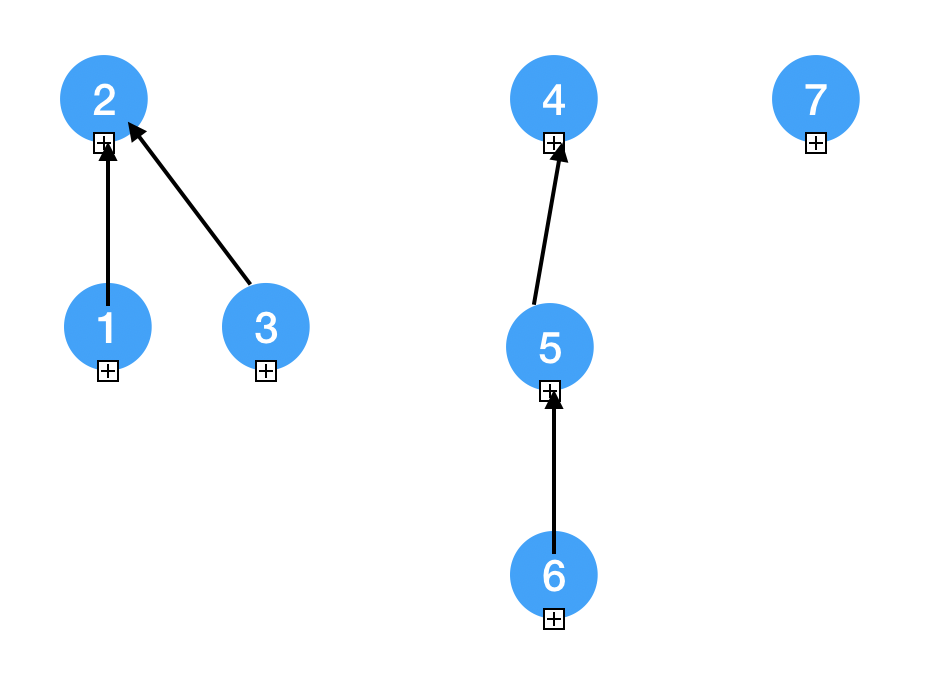
1 | 1 2 3 4 5 6 7 |
PseudoCode
1 | Find(u) { |
Union By Rank
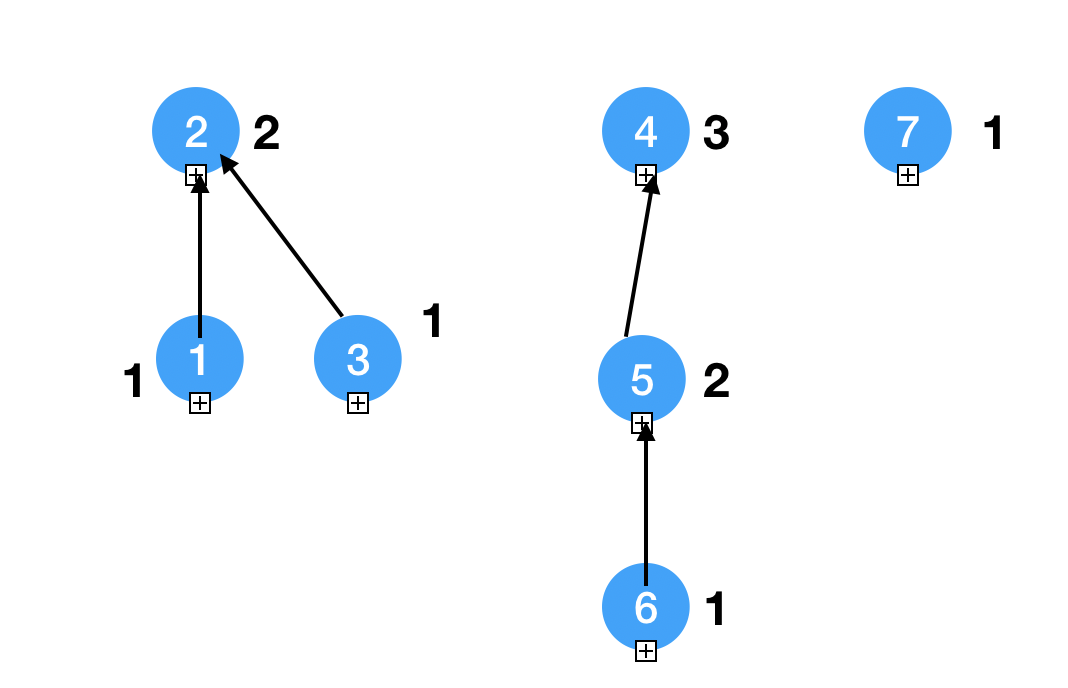
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/**
1 2 3 4 5 6 7
1 2 1 3 2 1 1
Find O logn Union O 1
num of item of a root node >= 2 ^(rank - 1)
proof:
if rank = 1, then 1 >= 2^1 - 1
assume rank = k, node >= 2^(k-1)
when rank = k+1, assume target = 2^k, we have node + node >= 2^(k-1) * 2 = 2^k >= target. Thus the time complexity is O logn
**/
// we need to find first
u = find(u);
v = find(v);
if (rank[u] < rank[v]) {
parent[u] = v;
} else if (rank[u] > rank[v]) {
parent[v] = u;
} else {
parent[u] = v;
rank[v]++;
}
Path Compression
We dont want a long chain here, we want less levels of nodes. So we modify the parent of the node to be the root each time we find.
Assume for a sequence of m U&F operations.
overall running time , O(mlog*n).
eg.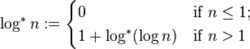
log 2 = 1
log 4 = 2
log 16 = 3
log 65536 = 4
log* 2^65536 = 5
1 | Find(u) { |